Beschreibung
Der Unterricht, die Lehrbücher und Lernmaterialien der konstruktiven Geometrie in der Ebene sind methodisch und didaktisch stark von der Umsetzung der Konstruktionen mittels Zirkel und Lineal geprägt. Das ist einerseits historisch bedingt als notwendige Vorbildung für die in diversen Berufen angewendete Darstellende Geometrie, andererseits aber auch fachdidaktisch, da sich die euklidische Axiomatik (resp. die hilbertsche moderne Fassung) perfekt mit diesen beiden Werkzeugen modellieren lässt.
Für die Untersuchung von Gesetzmässigkeiten im Klassenverband, zur Illustration von Beweisführung wie auch für Musterlösungen setzen wir Lehrpersonen jedoch häufig auf dynamische Software (GeoGebra), die hier wesentliche Mehrwerte liefert. Aus einer konstruktivistischen Perspektive erscheint es uns sinnvoll und überfällig, die Schülerinnen und Schüler auf diesem Werkzeug ebenfalls zu schulen, damit sie selbst zu Entdecker:innen der Geometrie werden können. Umgekehrt scheint uns die Fertigkeit, Konstruktionen formal korrekt und präzise mittels Zirkel und Lineal umzusetzen, aufgrund der geänderten technologischen Voraussetzungen ausserhalb des Geometrieunterrichtes nicht mehr relevant.
Aufgrund dieser Überlegungen wollen wir die Lehrplaninhalte der konstruktiven euklidischen Geometrie in der Ebene nicht mehr auf einem Papier mit Zirkel und Lineal modellieren und ausbilden, sondern in einer beliebig grossen (hypothetischen) Ebene mit klar definierten Konstrukten und Aktionen. Ein solches Modell wie auch die entsprechenden Werkzeuge liefert die Software GeoGebra.
Um den potenziellen Mehrwert auch abschöpfen zu können, reicht es nicht, nur das Instrument zu ersetzen. Es müssen didaktische Anpassungen formuliert und methodisch neue Umsetzungen entwickelt werden, Übungsmaterial angepasst oder erweitert und Instruktionen umformuliert werden.
Gleichzeitig muss dem Wegfallen der motorischen Handlung Rechnung getragen werden, da sie auf kognitionspsychologischer Ebene den Lernprozess unterstützt und von Schülerinnen und Schülern als kreativer und motivierender Prozess erlebt wird. Hier gilt es, zweckdienliche motorische Ersatzhandlungen zu entwickeln. Indem wir den zeichnerischen Skizzen einen wesentlich prominenteren Platz in der Geometrie einräumen, hoffen wir, dies sinnvoll abdecken zu können.
Innovationspotential
Das Projekt unterstützt Schülerinnen und Schüler bei ihren Lernerfahrungen mit digitalen Medien und begleitet ihre ersten Anwendungen mit einer mathematisch-geometrischen Software. Es trägt damit mediendidaktisch zur Digitalisierung des Unterrichts und zur medienpädagogischen Ausbildung der Schülerinnen und Schüler bei.
Unterrichtsentwicklung
Mathematische Software wird im gymnasialen Mathematikunterricht grösstenteils als operatives Hilfsmittel (wie Taschenrechner, Graphenzeichner oder Gleichungslöser) oder zur Schulung des Werkzeugs an sich (beispielsweise Tabellenkalkulationen oder Statistiksoftware) eingesetzt.
Wir vermuten jedoch ein grosses didaktisches Potential im Einsatz digitaler Werkzeuge, sobald die Schülerinnen und Schüler mathematische Fragestellungen dank digitaler Hilfsmittel explorativ untersuchen können.
Unser Projekt zielt in diese Richtung und leistet so Pionierarbeit für die Weiter- oder Neuentwicklung von digitalen didaktischen Konzepten in anderen mathematischen Themenfeldern.
Didaktisch-methodisches Konzept
Das Projekt findet in der Unterstufe des Langgymnasiums statt. Um die Vergleichbarkeit der Inhalte während der Probezeit gewährleisten zu können, setzen wir erst nach der Probezeit im Semester 1.2 ein. Geometrische Grundkonstruktionen und wesentliche Symmetriekonstruktionen werden somit weiterhin mit Zirkel und Lineal umgesetzt.
Inhaltlich erfüllen wir die Grobziele und Inhalte des Lehrplans des Realgymnasiums Rämibühl für die 1. und 2. Klasse, allerdings unter Ersetzung zweier Grobziele:
- aus «ebene Figuren mit Zirkel und Lineal konstruieren» wird neu «ebene Figuren mit definierten Methoden konstruieren» und
- aus «Konstruktionswerkzeuge gewandt einsetzen und exakt arbeiten» wird neu «Geometriesoftware gewandt einsetzen»
Im didaktischen Aufbau und den untersuchten Objekten orientieren wir uns stark an den gängigen Lehrmitteln (Geometrie 1 DMK), um bei Wechseln und Übertritten ein übertragbares Vokabular und einen vergleichbaren geometrischen Erfahrungsschatz gewährleisten zu können. Änderungen, Erweiterungen oder Streichungen von Aufgabenbereichen werden auch mit Bezug auf obiges Lehrmittel dokumentiert.
Ziel dieses ersten Blocks “Grundkonstruktionen” ist neben den geometrisch-inhaltlichen Zielen auch das Entwickeln einer Arbeitsroutine an der Software. Methodisch erfordert die Erarbeitung der Konzepte dynamischer Geometriesoftware für Schülerinnen und Schüler wie auch die Entwicklung einer Routine im Handling von GeoGebra viel Zeit. Ebenso dürften auf den verschiedenen Geräten einige technische Hürden zu meistern und viel individuelle Betreuung zu leisten sein. Beides spricht für einen stark auf Selbstlernmechanismen und Schüler:innenaktivitäten ausgerichteten Unterricht. Um ein hohes Mass dieser Unterrichtsform bieten zu können, fokussieren wir im ersten Block stark auf Methoden wie Selbstlernaufgaben, skriptbasiertes Lernen oder Unterstützung durch Lernvideos.
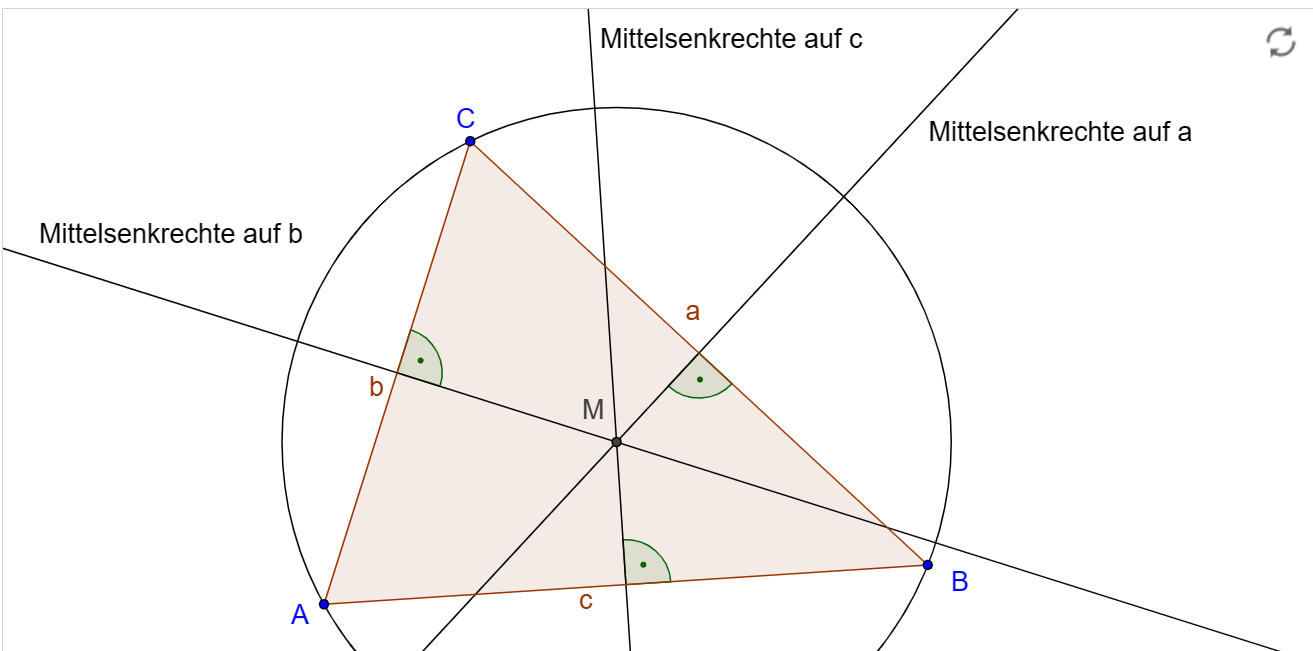
Im zweiten Teil “spezielle Linien und Punkte im Dreieck” wird die Software zum Hilfsmittel "abgestuft”, die Übungen und Aufträge nutzen die neuen Möglichkeiten, fokussieren aber nicht mehr das Medium oder das Kennenlernen spezifischer Tools. Die klassische Nutzung der Software zur Lösung und Illustration geometrischer Probleme steht hier im Mittelpunkt.
In einem möglichen dritten Teil steht die kreative Nutzung im Zentrum. Die Software soll auch ohne explizite Anweisung genutzt werden. Wir können uns hier offene Aufgabenstellungen, Beweisdiskussionen oder kleine Projektarbeiten vorstellen.
